Route finder
This is a uLisp program to find the shortest route between two places. This program illustrates an important problem that needs to be solved by every car navigation system, and could be used as the basis for a robot navigation program, to find the shortest route through a maze.
It is too large to run on an Arduino Uno.
Defining the map
The map program stores the map as a list of roads, where each road interconnects two locations. Here's the map we'll use to test the program:
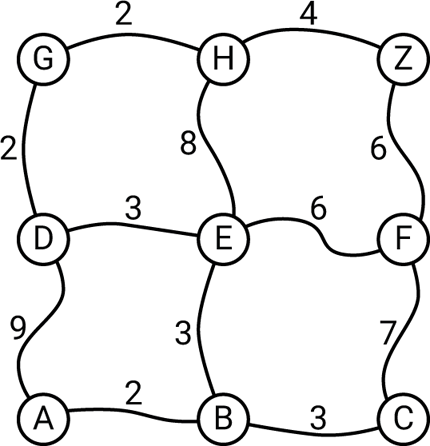
For simplicity each location has a one-letter name, such as A. The numbers show the time, in minutes, to get along the road between each pair of locations, and our goal is to get from A to Z by the quickest route possible.
Before looking at the answer below see if you can find the shortest route by hand.
Entering the data
The map data will be stored in a global variable called *map-data*, which we define as:
(defvar *map-data* nil)
(from to time)
where from and to are the locations at each end of the path, and time is the time to get between the locations. For example, the first path on the above map is:
(a b 2)
Here's the procedure add-road to add a path to the database:
(defun add-road (from to time) (push (list from to time) *map-data*) (push (list to from time) *map-data*)))
> (add-road 'a 'b 2)
((b a 2) (a b 2))
Maintaining a queue
Now that we can enter the map, how is the program going to find the shortest route? The technique is called an "ink-blot" or "breadth-first" search. It is like pouring ink into the starting location, and watching it spread out uniformly along the network, colouring each location as it reaches it. The shortest route to the destination location will be the route taken by the river of ink to arrive first.
To do this we will keep a list of the paths the ink is flowing along, arranged so the location reached first gets processed next. An ordered list of this sort is called a priority queue. We will store the entries on the queue as:
(time location from)
where time is the total time taken from the starting point, location is the location reached by the ink blot, and from is the location we've come from.
Here's the procedure add-item to add an item to the correct position in the queue, and return the new queue:
(defun add-item (item queue)
(if (null queue)
(cons item queue)
(if (< (first item) (first (first queue)))
(cons item queue)
(cons (first queue) (add-item item (rest queue))))))
For convenience we also have the following procedure adq (add-to-queue) that takes the priority-queue as the fourth parameter, and returns the updated queue:
(defun add-to-queue (time location via queue) (setq queue (add-item (list time location via) queue)) queue)
For example, if we want to add the road
(3 e f)
to the queue:
((2 a b) (4 c d))
we do:
> (add-to-queue 3 'e 'f '((2 a b) (4 c d))) ((2 a b) (3 e f) (4 c d))
Processing a new location
When the ink reaches a new location we want to add all the paths extending from that location to the queue. This is done by the routine add-roads, which adds all the paths leading from our current location to the queue, and returns the new queue:
(defun add-roads (location start queue)
(dolist (item *map-data* queue)
(let* ((from (first item))
(to (second item))
(time (third item)))
(when (eq from location)
(setq queue (add-to-queue (+ start time) to location queue))))))
It works as follows:
For every entry in the map data:
- If the from item in the map data matches our current location, add the road to the queue, with the time added to our starting time.
Growing the search
We are now ready to write the main procedure grow for growing the ink from the starting location until we reach the destination. We will return a list of all the locations encountered as the ink spreads, and the location we came from:
(defun grow (from to)
(let* ((visited (list (cons from nil)))
(queue (add-roads from 0 nil))
w)
(loop
(when (eq from to) (return (reverse visited)))
(unless queue (return))
(setq w (first queue))
(setq from (second w))
(setq queue (cdr queue))
(unless (assoc from visited)
(setq visited (cons (cons from (third w)) visited))
(setq queue (add-roads from (car w) queue))))))
To see how grow works let's set up a very simple map:

Clear the map data:
> (setq *map-data* nil) nil
> (add-road 'a 'b 2) ((b a 2) (a b 2))
Add the road between B and C:
> (add-road 'b 'c 1) ((c b 1) (b c 1) (b a 2) (a b 2))
Then grow the ink blot until we reach the destination "C":
> (grow 'a 'c) ((a) (b . a) (c . b))
The procedure grow returns a list of the locations visited, and in each case the location we came from.
To complete the project we need to create the actual route from this list of locations visited.
Listing the route
Here is the procedure list-route to call grow and list the route:
(defun list-route (from to)
(let* ((visited (grow from to))
route)
(when visited
(loop
(push to route)
(when (eq from to) (return route))
(setq to (cdr (assoc to visited)))))))
Example
Let's try out the route map program to find the shortest route through the map at the beginning of this section. Here's a procedure make-map to define the map:
(defun make-map () (add-road 'a 'b 2) (add-road 'b 'c 3) (add-road 'a 'd 9) (add-road 'b 'e 3) (add-road 'c 'f 7) (add-road 'd 'e 3) (add-road 'e 'f 6) (add-road 'd 'g 2) (add-road 'e 'h 8) (add-road 'f 'z 6) (add-road 'g 'h 2) (add-road 'h 'z 4))
So we execute:
(setq *map-data* nil) (make-map) (list-route 'a 'z)
The answer comes back:
(a b e d g h z)
If you investigate you'll find that this is indeed the shortest route from A to Z.
Here's the whole route finder program: Route finder program.
